The A – Z of Music: K

Aged only 19, Kate Bush stormed to the top of the UK charts with the self-written Wuthering Heights. It’s based on the classic Emily Brontë novel of the same name. It’s really quite unlike anything else – Kate twirling around like a woman possessed, with that high-pitched, ethereal squeal coming out of her. It’s barmy, literary, and utterly enchanting:

A C. S. Lewis Related Joke

I looked in my wardrobe today, and found a Lion and a Witch. I asked them what they were doing there, and they replied, “It’s Narnia business.”

Nelson Mandela, 1918 – 2013

.

Nelson Mandela died today.

He devoted his life to ending Apartheid in South Africa, at a personal cost of 27 years imprisonment. He achieved his aim, and was the first democratically elected and black President of that country.

He dies lionized by all.

P.S. Nelson Mandela was portrayed in a film called Invictus. Which happens to be the name of a poem by William Ernest Henley, which could almost have been written for Mr. Mandela:

Out of the night that covers me,
Black as the Pit from pole to pole,
I thank whatever gods may be
For my unconquerable soul.

In the fell clutch of circumstance
I have not winced nor cried aloud.
Under the bludgeonings of chance
My head is bloody, but unbowed.

Beyond this place of wrath and tears
Looms but the Horror of the shade,
And yet the menace of the years
Finds, and shall find me, unafraid.

It matters not how strait the gate,
How charged with punishments the scroll,
I am the master of my fate;
I am the captain of my soul.

The Wheat and the Chessboard

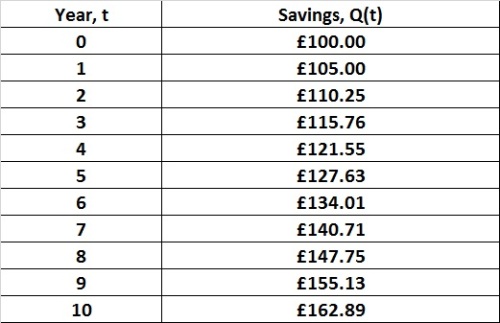
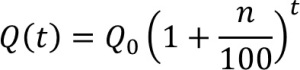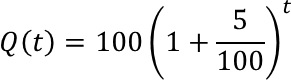In the last post, we saw an example of exponential growth: where something gets multiplied by the same amount again and again and again. When things grow exponentially, they grow very large indeed. Here’s a famous story which illustrates this:

The inventor* of chess** brought his invention to the King, who was so impressed he offered any prize the inventor asked for. The inventor offered the King a choice. He could either pay him 10,000 rupees, or make a payment of wheat based on the squares on the chess board.

To pay in wheat, the King would have to place 1 grain on the first square, 2 grains on the second square, 4 on the third, 8 on the fourth, and so on; doubling the number of grains each square.

The King, who didn’t know his maths, couldn’t believe he was being asked so little and promised to pay in wheat. Bags of wheat were brought in, and a grain placed on the first square, 2 on the second etc. Before long, the first bag was empty and another was called for. That bag soon ran out, and another, and another.

It soon became obvious that more wheat would be needed than in the whole Kingdom!

Some versions of the story say the inventor became the new King, others that the inventor was punished***. We can work out how many grains of wheat the King needed.

The number of grains on the:

1^st square is:                                                                                                      1 grain

2^nd square is:                         1 × 2 =                1 × 2¹ =                                2 grains

3^rd square is:                  1 × 2 × 2 =                1 × 2² =                                 4 grains

4^th square is:            1 × 2 × 2 × 2 =               1 × 2³ =                                  8 grains

…

n^th square is:                                                      1 × 2ⁿ =                                2ⁿ grains

.

Adding these gives:     1 + 1 × 2¹ + 1 × 2² + 1 × 2³ … which is a geometric sequence (click Continue Reading→  at the bottom of the post for a fuller discussion of this).

Given there are 64 squares on a chess board, we can find that the King would have needed 18,466,744,071,709,551,615 grains of wheat! No wonder he didn’t have enough!

An Equation You Can Bank Upon

In his best-selling book A Brief History of Time, Stephen Hawking wrote:

Someone told me that each equation I included in the book would halve the sales. I therefore resolved not to have any equations at all. In the end, however, I did put in one equation, Einstein‘s famous equation, E = mc². I hope that this will not scare off half of my potential readers.

Since I’m the only one who ever reads this blog, and I can’t scare off half of myself, I’m going to plough right in and put an equation into this post.

It is an equation that the lecturer has talked about a few times in the Calculus course:

.

Now that may not mean much to you, but it is saying that if we start off with some number Q₀, which grows by n% a year; then after t years, it will grow to Q(t)*.

This equation could represent the money we put into a bank account that pays interest each year. For example, if I put in £100, and then get paid 5% interest each year**, then Q₀ becomes 100 and n becomes 5:

.

Now our equation is simple to interpret***. If we want to know how much money will be in our account in 1 year’s time****, Q(1), we put t = 1 into our equation and see what pops out. Putting t = 2 will tell us how much will be there in 2 years time, Q(2). We can then put t = 3 for 3 years, t = 4 for 4 years etc.

Rather than work it out by hand for each year, one can put the equation into spreadsheet software, like Microsoft Excel, and work out how much we will have in our account so many years from now:

So in just 10 years, our £100 has become almost £163 – just under two-thirds as much again. This is the miracle of compound interest and why it pays to have savings or other financial assets to make money for you. No more by the sweat of your brow will you eat, but by the sweat of others.

The A – Z of Music: J

Here’s Joan Armatrading with Love & Affection. You know that’s what I like:

P.S. If a bad song with a sax solo exists, I’ve yet to hear it.