Bayes Watch

I hope the title hasn’t misled you. I’m afraid this post is about probability, not Pamela Anderson.

It won’t be too technical, and will draw on a really important real-life application. Take the example of routine screening for breast cancer, where all women of a certain age are given a mammography to test for the disease. Imagine you were given the following information:

The probability that one of these women has breast cancer is 0.8%. If a woman has breast cancer, the probability is 90% that she will have a positive mammogram. If a woman does not have breast cancer, the probability is 7% that she will still have a positive mammogram. Imagine a woman who has a positive mammogram. What is the probability that she actually has cancer?

Don’t worry if this leaves you hopelessly confused – so was I when I first encountered this problem. I guessed an answer of around 90% – after all it says if you have cancer there is a 90% chance you’ll get a positive mammogram. But that’s the probability of you having a positive test given that you have cancer. The question asks, what is the probability of you having cancer given that you have a positive test. It turns out there’s a huge difference between the two.

The difference is that sometimes you can have cancer and still get a negative test (this is a false negative). If 90% of those with cancer get a positive test, that still leaves 10% of those with cancer getting (wrongly) the all clear. You can also not have cancer and still get a positive test (this is a false positive). As it says, 7% of those without cancer will be told they have it. No test is a 100% accurate; human error can creep in and samples get mixed up, the technology malfunctions etc.

One way of making the problem a little easier to solve is to eschew the probabilities and %’s, which people find hard to understand, and just count the number of times things happen. If we translate our above problem as follows using frequencies:

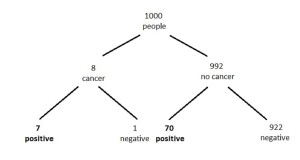
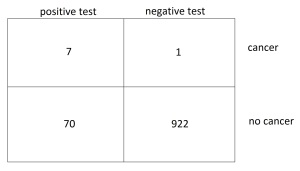
8 out of every 1,000 women have breast cancer. Of these 8 women with breast cancer, 7 will have a positive mammogram. Of the remaining 992 women who don’t have breast cancer, some 70 will still have a positive mammogram. Imagine a sample of women who have positive mammograms in screening. How many of these women actually have breast cancer?

This is exactly as before. But we say 8 out of 1,000 rather than 0.8%, even though they mean the same thing. Reading this, it becomes easier to solve the problem. Counting those who get a positive mammogram, we see there are 7 + 70 = 77. But only 7 of these have cancer. So the chances of you having cancer if you get a positive mammogram is 7/77 or about 9%.

This is quite small. Why? Well, even though 90% of those with cancer got a positive test, there was only a small number with cancer to begin with (8 in fact). A large percentage of a small number still gives you a small number. Meanwhile only 7% of those without cancer got a positive test. But there were a large number of women without cancer (992). A small percentage of a large number gives you a large number. It was this large number that swamped the small number – the number of false positives outnumbered the true positives, and so only a small proportion of those with positive tests actually have the disease.

So this is immensely important. If ever you get a positive test for a disease, remember it doesn’t necessarily follow you have the disease. Depending on the number of false negatives and positives, you might have a very small chance of actually having the disease you’ve tested positive for. Many people’s world’s have fallen apart because they have been told they test positive for a disease, be it breast cancer or HIV. But they, or their doctors, never stop to think that many people can still get a positive test even though they don’t have the disease. In our example above, most of the women with positive tests didn’t have the disease (70 without cancer versus 7 with). If this was explained to them, they could realise that a positive test is not conclusive. They could find out a bit about the probabilities that you actually have the disease or that the test has misled you in this case, and maybe ask for more tests.

Either way, you know that a positive test shows you have the chance of having the disease, it’s not a death sentence. You’d feel a lot better knowing that a positive mammogram meant there was a 9% chance of having breast cancer, not a 90% one.

Unfortunately, research has been taken on how many doctors understand all this reasoning, and scandalously few do. They studied medicine, not statistics after all. If ever you get a positive test, press your doctor on these points to ensure you are getting the right information.

A picture tells a thousand words: Sometimes pictures help work these problems out. One can draw a tree diagram:

This shows more clearly the 77 with positive tests, of whom only 7 have cancer.

You can also ‘think inside the box’:

A little bit more: I realise I haven’t yet explained the title. The type of probabilistic thinking used in this post is called Bayesian probability, named after Thomas Bayes, a Presbyterian minister who did work in mathematics. I won’t go into too much detail (I don’t understand a lot about it myself), but it gives a way of telling us how we should update our beliefs given the evidence we find.

In the above breast cancer screening example, we wanted to find how much the evidence (the mammography test) should lead us to believe we had cancer. It can be applied to any of our beliefs and the evidence we hold for them.

The example I’ve used comes from an excellent book, Gerd Gigerenzer‘s Reckoning with Risk:

From Here to Eternity

A post-church pub discussion led to me and a friend speculating about Heaven.

It’s a subject that lends itself to speculation, as there is no hard-and-fast evidence that anyone can show you about what Heaven is like, or that it exists. Christians believe that its existence and certain other of its characteristics have been revealed to us from God, and we take these on faith. But there’s still an awful lot left hanging about what it’s like.

Some of the missing details I wondered about:

• What’s the state of technology in Heaven? It says in the Bible that there are roads and gates, and other made things. Will there be televisions or kettles, sheds or computers? Will we have cars or planes to get about in – or will we be able to fly or teleport unaided?
• Will all the works of art made over human history – be they books, or paintings, or films – be available to us in Heaven? Will we be able to get around to reading all the books we wished we’d read, or watch those TV shows that always clashed with other things? My friend thought not, as all human art will contain sinful things like death, hate and lust that will have no part in the new creation. I thought this was a shame, as often great art deals with nasty things.
• Will we know everything in Heaven? It sounds nice if we did, but then we’d lose the thrill of discovery and scientific advancement and the hard but rewarding slog of reducing the extent of our ignorance.

You might think these are all trivial thoughts around such a big subject (- I suspect many more of you will think I’m deluding myself that such a place exists), for there are far more important questions, and there will be far greater things to concern ourselves with there, but these seem important to me. Anyway, I’m sure I’ll know one way or the other one day.

Economics, Part 1, Chapter 3

Here is the next instalment from the ‘Economics‘ textbook. It covers the concepts of supply and demand – concepts which are very simple, yet help us understand a lot about how economies function.

If you read it, you should understand why strict anti-drugs laws make drug-dealing so lucrative, and why you would have got a nice pay rise if you survived the Black Death!

.

As this is the last Chapter in Part 1, I’m going to take a break before starting on Part 2. That’s not to say I might not expand upon this Chapter in following posts.

The A – Z of Music: E

With famous birthdays all over the news this week, I thought I’d look to see what song was No. 1 when I was born. It turns out it was Madonna‘s Into The Groove – well, not my favourite song. But the previous No. 1 was There Must Be an Angel (Playing with My Heart) by Eurythmics. It’s got an angelic-looking Annie Lennox, a falsetto-ing fatty, and Stevie Wonder doing a harmonica solo. What more could you want from a music video*?

A Name Fit For A King

What’s in a name? That which we call a rose by any other name would smell as  sweet

Romeo and Juliet

With the royal baby born, the next thing everyone wants to know is what name will it be given. I can predict this no better than anyone else, and have no strong opinions on what I’d like it to be called – although I’m sure such excellent suggestions as King Ralph, King Kong, and King S’of’Leon will be ignored.

We’re on much stronger ground when it comes to what past Kings and Queens are called, and in case you’re a little rusty on this:

P.S. The clip is from CBBC‘s fantabulous Horrible Histories television show – which were taken from a series of books of the same name by Terry Deary. I have a nearly-full collection of these books that I started getting when I was 11. They’re an excellent, and fun, way of getting children to learn about history.

Royal Baby Born!

BREAKING!: Will & Kate have had a baby boy. Live scenes from outside St. Mary’s Hospital:

Irreverence aside, I wish the baby boy well. It will share a birthday with my little sister, who became 10 today. If he turns out half as well as she has, we’ll have done well.

Jesus Walks, Jesus Walks With Me

A miracle happened last night.

I was out with the Plymouth Street Pastors. As usual, before we went out on our first shift, we had a group prayer. We were told that as we were out on the streets, Jesus would be there with us.

Now, within 10 minutes of starting out, I kid you not, we were passed by a young man with long hair, a beard, white robes and a crown of thorns! I’ll grant you, the tin of Fosters in one hand was a little incongruous, as was the plastic bag of shopping in the other. His clothes had a vague hint of cheap fancy dress shop origins. But still, I’ll take my miracles where I find them.

For those that don’t know, Street Pastors are a group of volunteers from different churches who gather together on a Saturday night and patrol the main nightlife areas. As anyone who’s visited a typical British town late on weekends, there’s plenty to keep an eye on. The drink flows pretty freely, so there’s plenty of opportunity for people feeling sick, having fights, getting teary and emotional and arguing with partners, and unfortunately even deaths and sexual assaults.

An artists impression of Plymouth’s nightlife on a Saturday night*

When we’re out, we can do a lot of good. We carry with us a big bag where we keep first aid kits, a dustpan and brush to sweep up broken beer bottles, drinks of water for the worse-for-wear, and (what we’re best known for) flip-flops for those slightly inebriated, stumbling young ladies in high heels.

We can also be a great preventative measure. If you see a group of people in uniform nearby, you might think twice about throwing that punch, or following that young lady down the dark alley.

We’ve also saved several lives. A couple of people have been resuscitated by Street Pastors. Our medical help (or at least our calling of ambulances) has prevented deaths. Several suicides have been prevented by our interventions.

But many hundreds of people have benefited us in smaller but no less important ways. We’ve been the shoulder to cry on, or the person to help you into a taxi, or to wait with you until your friends can find you.

We’re really appreciated by the people out of the town, which makes walking the streets until 4am seem worthwhile!

P.S. The title of the post is, following this blog’s tradition of never-knowingly up-to-date cultural references, from a Kanye West song.

The A – Z of Music: D

My posts this week have been a bit technical and heavy, so here’s some light entertainment. The next instalment in my A – Z of music.

It’s going to be Dexys Midnight Runners, Come On Eileen. I just remember hearing it a lot at family dos when I was very young – and it’s a great song.

Externalities

The tinny sounds of Greensleeves comes floating through your window. Your parents place a couple of pound coins in your palm before you run out. A brief conversation with the ice cream man concluded, your hands lose the pound coins only to gain a couple of 99s a few minutes later. The ice cream man’s happy; the money being enough to compensate him for his ice cream and the time spent driving in his van past your house. You’re happy, there’s few better things to spend your money on a hot summer’s day. Your neighbours aren’t happy though – their getting a bit fed up with the tinny sounds of Greensleeves.*

This isn’t pointless nostalgia. I’m describing a negative externality**. In the above market transaction, the buyer and seller are happy (they wouldn’t have made the trade else). The seller’s costs are met, the buyer gets the benefits they paid for. But people outside (external to) the transaction aren’t happy – the neighbours get the costs of hearing the noise without being paid for it.

Dealing with these externalities is a legitimate cause of government intervention in the market. They may deal with such negative externalities by regulating it, such as the rules on ice cream vans playing music. Or it may be possible to make people pay for the external costs (an ice cream van tune tax anyone?)

But maybe the way to deal with these market failures is… more markets.

Let’s take the ultimate negative externality – pollution leading to global warming. The argument is we all pay for our lovely factory-made consumer goods and drive our cars; while, in order to do so, burning fossil fuels, pumping greenhouse gases into the atmosphere, heating the globe, melting the ice caps, causing the sea level to rise and ensuring many of us will be sharing our homes with the fishes in a few centuries’ time.

One option is to regulate greenhouse gas emissions, like CO2, just as we regulate ice cream vans. Ban dirty factories and cars. Set limits on how much we pollute. All very well, we do need limits. But its a bit of a blunt instrument. Some industries, like producing steel, are inherently polluting. If we regulate it too much, it will just up shop and move to where environmental standards are laxer. Meanwhile, it doesn’t provide much incentive for those who aren’t near the polluting limit or who could easily cut their emissions.

Instead, the government could decide on how much CO2 emissions it will allow, and then give everyone a right to emit so much each – a pollution permit, if you will. Not only that, but it could allow people to buy and sell the permits. We would have a market in pollution. This is emissions trading or cap-and-trade, as the government first caps how much emissions it will allow.

The big, dirty factory won’t have enough permits at the start to do its work. However, there will be many other companies who will never hope to emit as much CO2 as they are allowed. They’ll have permits left over which they can sell. The big, dirty factory can buy the left-over permits these non-polluters don’t need from them, and use it themselves.

Obviously, the factory now is having to pay to buy these extra permits, and so will stretch every sinew to pay as little as possible – that is, will try its darnedest to reduce its emissions. Meanwhile, those who are selling their unused permits will realise that they can get richer the less CO2 they emit, as they’ll have more left-over permits to sell.

Everyone now has the incentive to reduce their emissions – an incentive they can count in pounds and pence every day. But people can do so now with much more flexibility and discretion. Under simple regulation, those who found it hardest to adapt were forced to do so first, and probably went out of business as a result. Meanwhile those who could adapt most easily had no reason to do so. Under emissions trading, those who can reduce their emissions most cheaply and easily will. Society can meet the inevitable costs of avoiding climate change at the least cost to itself.

This isn’t an academic theory, such markets in CO2 emissions exist now. The first and largest is the European Union Emission Trading Scheme, which has had some teething problems***, but could end up showing the way. There are similar schemes in Switzerland, Australia, New Zealand and South Korea. There are also subnational schemes in parts of the US, Canada, and Japan. There was a very successful SO2 cap-and-trade scheme in the US, which helped prevent the Acid Rain problem.

So, sometimes little bits of economic theory might show the way to dealing with our most pressing problems.

P.S. There can also be positive externalities.  If you plant an apple tree in your front garden, your neighbour may get the benefit of its shade and its cast-off apples without having paid anything.

These positive externalities are like the public goods I discussed in my other post, The Logic of Collective Action. Benefits are bestowed that people need not have paid for, and so may not get paid for in effective amounts. The market on its own would produce too little of these benefits.

Let the Music Play!

I have just caught an episode of the Daily Politics show. There was an item on the restriction on ice cream vans* playing their music.

The reporter pointed out that no other vendors can use music in public to advertise their wares, and that we wouldn’t want to go back to Victorian times, where people would be out shouting in the street trying to sell their goods.

I blow his argument out of the water with a single video**: